Blog – Logic Low

Quarter Wave Debugging

When building a sine lookup table, you can use the symmetry of the sine wave to save lookup table resources. This seemed like a straightforward task but actually had an interesting problem. The sine wave below looks fine, but when compared to the actual waveform a period function appeared in the data.

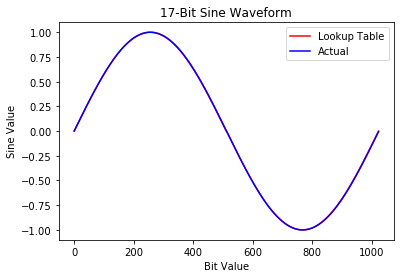
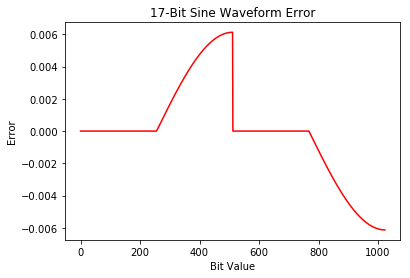
Simulation of the 1/4 wave lookup table vs the real value.

Error comparison of the two waveforms above.

The crux ended up being phase quantization. This is shown clearly when the table is reduced to an 8-deep table:

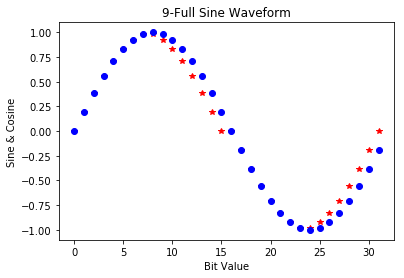
In the initial calculation the sine wave lookup table was based on the equation:

lookup_table(x) = sin((pi/2)*(x/lookup_table_size))

Which resulted in the plots above. While this error probably doesn’t matter much for my application, I was a bit confused by it. I hunted around a bit and found this website which went into detail about the problem and identified a solution which was a half phase slip using the equation

lookup_table(x) = sin((pi/2)((2*x+1)/(lookup_table_size*2)))

This results in a sine wave that’s been shifted, but is otherwise dead on the calculated version!

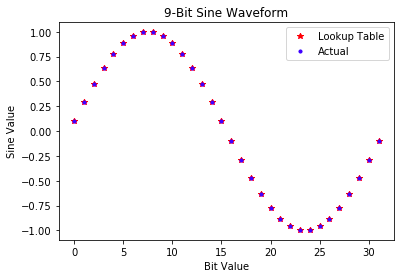
Which holds as the quarter wave table is expanded to its full scale, 256×16

Arts and Crafts

I decided FRED needed to stop sporting his old ASEA logo! Bring on the Bondo.

This was how the project started, the raised ASEA (the A in ABB) logo.

Time to start grinding:

Lots and lots of sanding

On both sides until

I did my best to find the font, even asking reddit.com/r/identifythisfont but no luck. Everyone thought it was a custom font. My friend who happened to love fonts used the original letters to generate:

I thought I might be able to use cardboard as a mold coated in wax, but as it started to take shape I knew there wasn’t a chance.

So I went to my helpful plastics place and asked them for a laser cut mold that was made out of a material that wouldn’t stick to Bondo. Turns out they know their plastics.

Then it was time to prime with an something that would etch the plastic slightly to allow the Bondo to bond’o.

Primed it was time to apply the base layer of Bondo to create an even surface for the lettering and to fill in any divots from the Dremel. I used a Bondo with long glass fibers for this step.

Once it was dry it was time to sand it smooth.

Once there was a smooth surface it was time to apply the mold!

My ‘holy crap it worked’ face

Both Sides

Time to polish it up

Then prime

FRED's new cap primed and ready for paint — FRED’s new cap primed and ready for paint

But then I thought, why should I paint my robot if my robot is build to paint?

Hacker paint booth

Painted! It was a fun experiment but ended up doing most of it by hand. If I needed to paint 11 thousand, I would have trained FRED a bit more, but since it was just the one, didn’t seem like a good use of time.

The Final Product

FRED At the Movies

A few months ago I was talking with Ben, the owner of Lyric theater here in Fort Collins. Ben was in the planning stages of the release party for Whensday, the first movie produced by the Lyric. Off hand I said we could have FRED there serving beers, wouldn’t that be fun?

Flash forward until a week before the event – Ben wants to know how the bartending robot is coming along.

“Oh it probably won’t be ready to pour beer by August” I say amused by the image.

Ben looks worried, “what? No. It’s got be there. Everyone is expecting to see a robot bartender.”

“Well then, it will be there.”

The general idea was he would pickup a solo cup from a stack using a two part suction cup then bring it to the kegerator which was activated by a solenoid from FRED’s control cabinet. It all worked great in the warehome but upon arriving at the Lyric for the premier, the solenoid refused to trigger and so FRED just ended up dancing (doing the robot) behind the human bartenders for the night. His mechanical dance moves were a hit.

Linux Bot

Took a few minutes tonight to rip apart an old Eeeeee PC knock-off and embed it within the robot. I was planning on just throwing my raspberry pi in there, but this thing was just gathering dust on the shelf and could probably use some love.

Over the next week I’ll throw together a simple serial interface board for the digital I/Os on the bot and a python interface to the web!

Anyway, here’s some pictures of the teardown and repurposing. Enjoy!

[warning_box] No science actually happened here. [/warning_box]